Background

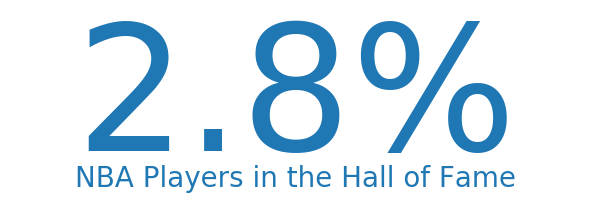
Out of all the outstanding players that have been in the NBA, less than three percent have been inducted into the Hall of Fame.

• Who should be next to receive this honor?
• Are there common measurable traits among Hall of Fame players?
• Is it possible to identify these top tier stars while they are still playing?

This project will apply machine learning techniques in search of the answers to these questions.

You're probably thinking, "What's the point?"

While singling out historical figures that deserve recognition for their accomplishments would contribute to the game, signing gifted athletes early in their careers to your team would lead to championships.

Strategy

There are a couple of obvious paths to learning what traits will result in exceptional players at the professional level.

1. Study the game of basketball for a lifetime to acquire expert knowledge.
2. Study players that are already in the Hall of Fame to learn what they brought to the court.

I possessed some talent in soccer during my youth, but was a complete liability on the basketball court. In lieu of dedicating the second half of my life to the art of round ball, let's choose option 2 and see what there is to find in almost 70 years of player statistics.

If you would like to investigate any of the datasets used for this project, check out the data files section below.

Links to all the source code and the project's Notebook are also available.

Exploratory Data Analysis

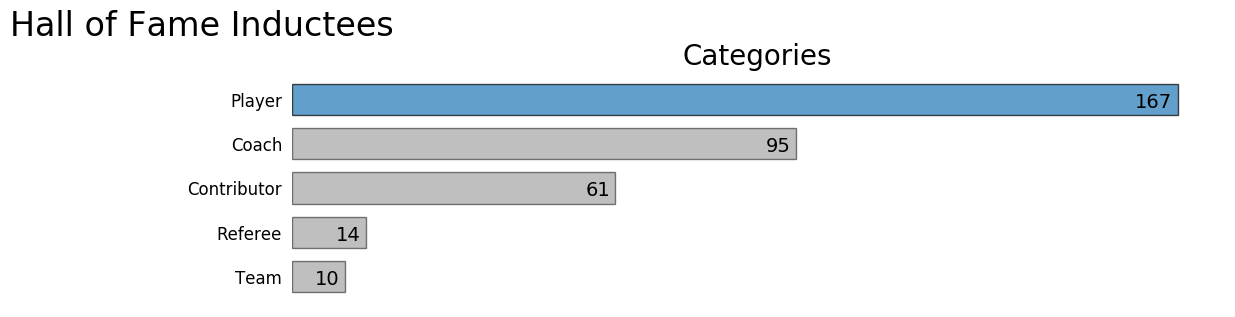
The Naismith Memorial Basketball Hall of Fame located in Springfield Massachusetts is where the best of the best are enshrined for history. There are a number of different ways to get into the Hall other than being a player, as shown in the graphic below.

Of interest is the fact that there are far fewer coaches at the pro level, but it appears they have a much higher percentage of being selected to join the Hall of Fame. So if your end goal is to be inducted into the Hall of Fame, coaching might be a better option than playing. One could also argue that getting a coaching appointment on a professional sports team is more difficult than getting in a game. The call on how to perceive that anomaly will be left up to you.

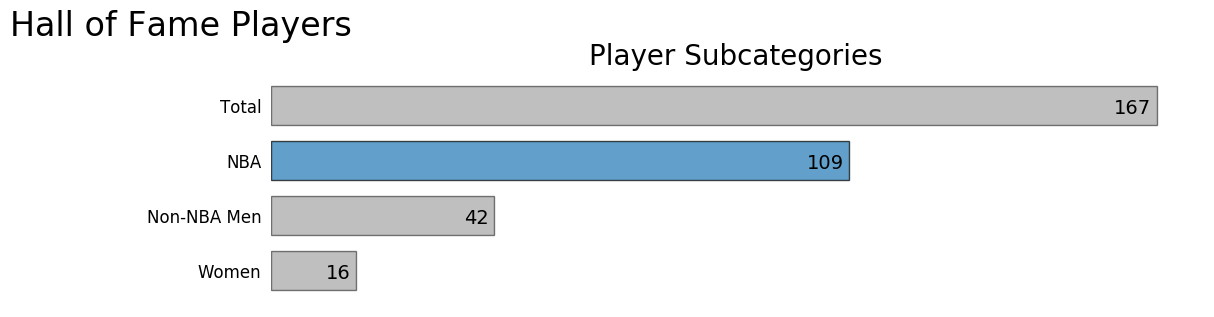
An important detail about the Naismith Memorial Basketball Hall of Fame is that it's for all Basketball. This means there are many player subcategories in the Hall.

• Collegiate athletes
• Greats from the women's game
• Historic figures who played prior to the formation of the NBA
• NBA Stars
• Players from leagues outside the United States

The next chart depicts a break down of the different player categories as of 2012. For this project, we are concentrating on the inductees that played in the NBA. That means the calibration data sample size is reduced from 167 to 109.

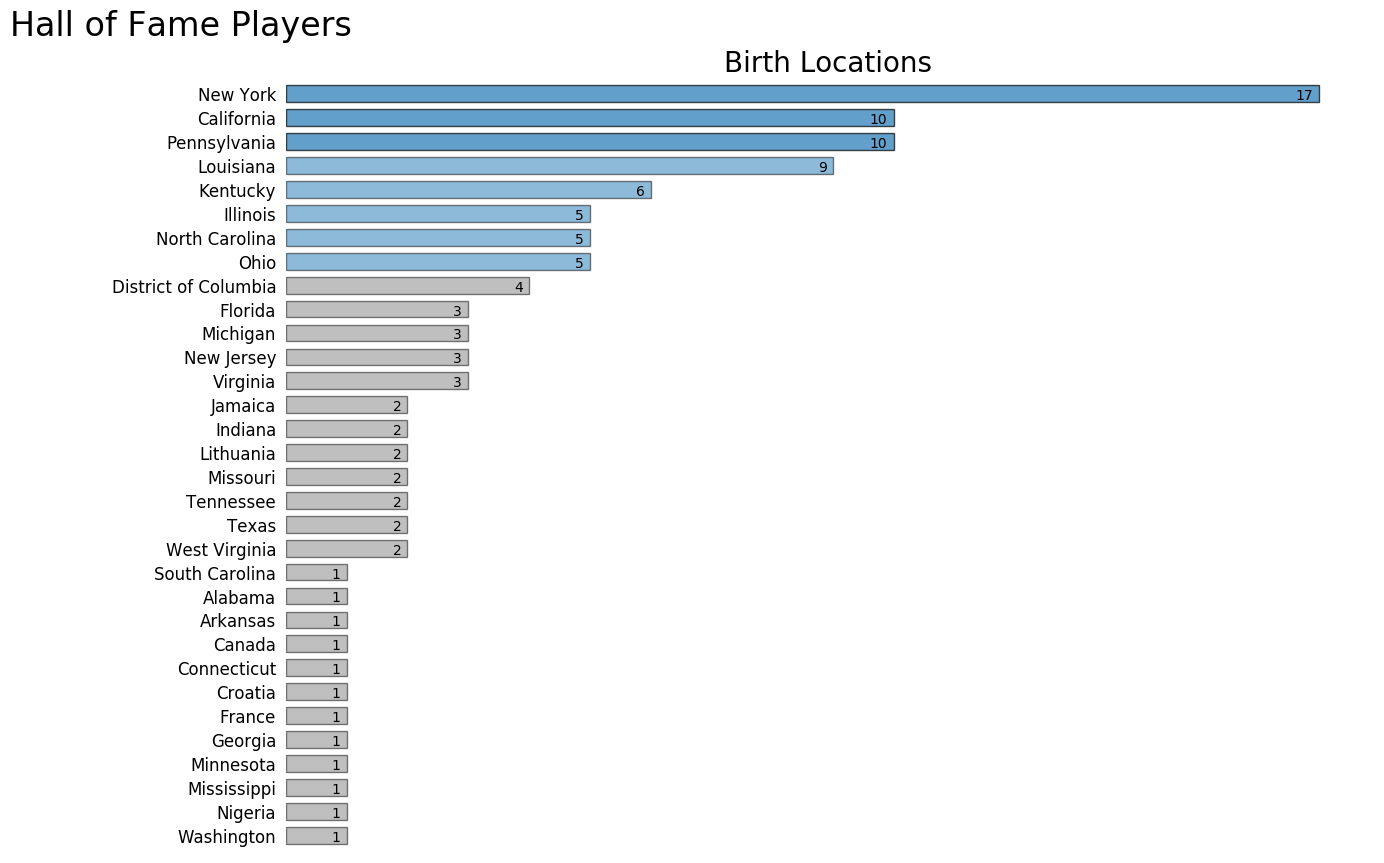
It's also interesting to note that NBA Hall of Famers come from very few places on the planet. New York State has produced more Hall of Famers than any other location. Countries outside the United States with inductees include Jamaica, Lithuania, Canada, Croatia, France, and Nigeria.

The next graphic lists the birth place of all the Hall of Fame players ranked by quantity in descending order.

On the map, each circle glyph is proportional in size to the number of Hall of Fame players from that location.

Use the buttons on the right side of the map to pan and zoom.

Another interesting fact about the players is the majority were members of collegiate teams. Until 1971 players had to exhaust four years of college eligibility to join the pros, but the entrance rules have changed multiple times over the years. As of 2006, any player declaring for the draft must be 19 years old and one year removed from high school.

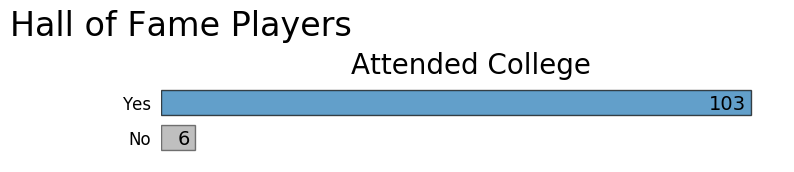
Now that we have some background information, let's dive in and see what knowledge is hidden away in the player statistics.

Analysis

The Season Statistics dataset contains 47 performance statistics for all NBA players going back to 1950. We are going to use these values to develop a predictive model to categorize if each season was Hall of Fame worthy or not. As the following correlation matrix displays, most of the linear relationships between the numerical variables are positive and some are significant.

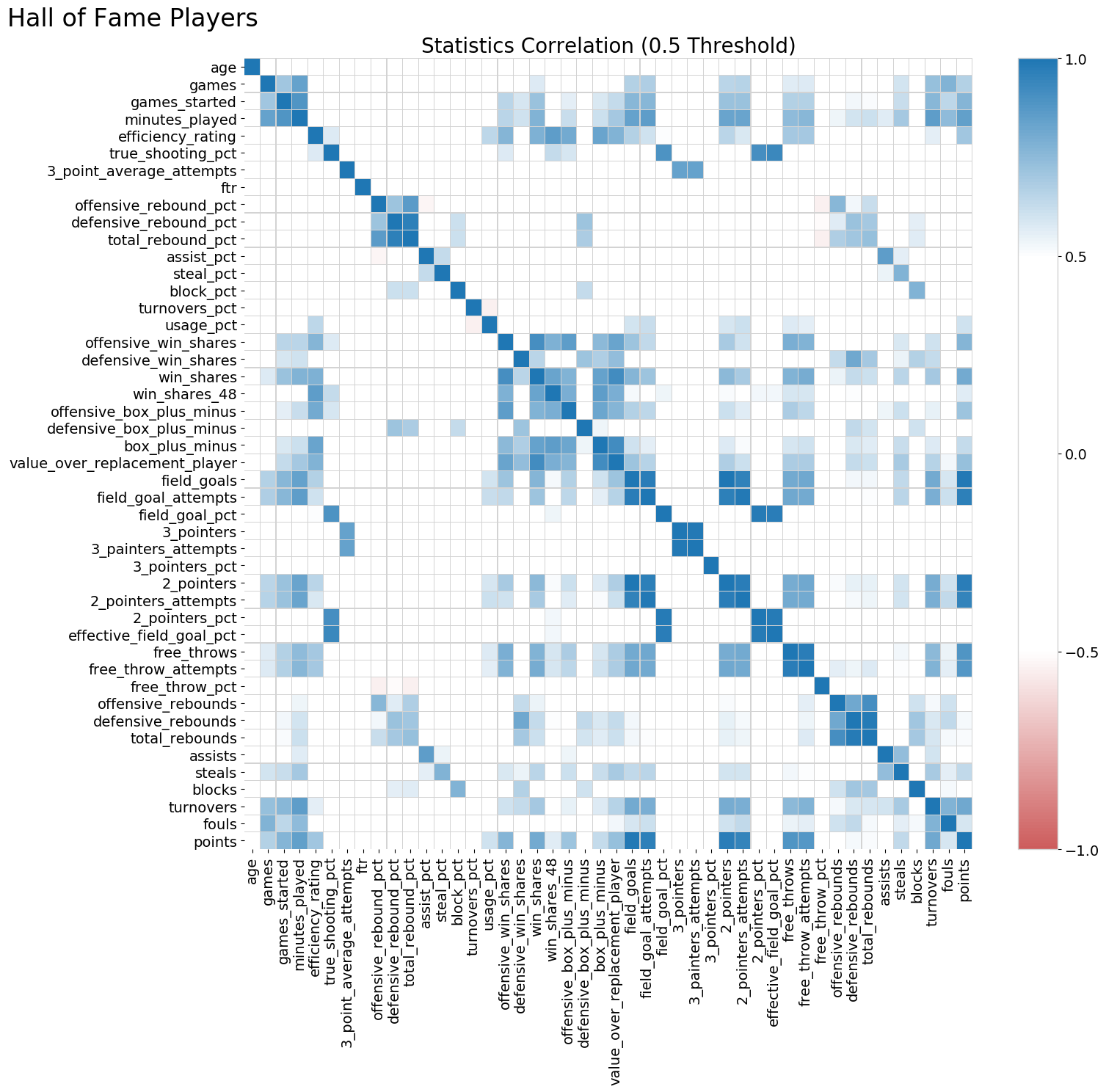
An added complexity of this dataset is values are logically missing from bulk portions of the records. For example, the three-point shot was introduced to the league in 1979. This results in every player's season prior to this date having a null value for this statistic.

A common approach to deal with these missing values would be to employ an imputer class to fill the holes with an aggregate function. Due to the mechanical nature of the null value locations, I chose not to utilize this technique. Instead, the data was partitioned into 21 unique subsets, each void of any null values. Why 21 you ask? This was the number of unique complete subsets that existed in the dataset. The following table breaks down which features are included in each subset.

Features	12	13	16	17	20	21	22	23	25	26	27	28	36	40	40	41	42	43	45	46	47	48
Samples	24624	24616	24577	24491	24478	24449	24137	23970	23970	23223	23970	23970	23223	21713	20746	19984	19984	18856	18856	18161	17486	14585
2-Point Field Goals	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
2-Point Field Goal Attempts	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
2-Point Field Goal Percentage						✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
3-Point Field Goals																			✓	✓	✓	✓
3-Point Field Goal Attempts																			✓	✓	✓	✓
3-Point Field Goal Average Attempts																				✓	✓	✓
3-Point Field Goal Percentage																						✓
Age		✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Assist Percentage											✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Assists	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Block Percentage															✓	✓	✓	✓	✓	✓	✓	✓
Blocks														✓	✓	✓	✓	✓	✓	✓	✓	✓
Box Plus Minus														✓	✓	✓	✓	✓	✓	✓	✓	✓
Defensive Box Plus Minus														✓	✓	✓	✓	✓	✓	✓	✓	✓
Defensive Rebound Percentage															✓	✓	✓	✓	✓	✓	✓	✓
Defensive Rebounds														✓	✓	✓	✓	✓	✓	✓	✓	✓
Defensive Win Shares			✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Effective Field Goal Percentage					✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Efficiency Rating									✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Field Goal Attempts	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Field Goal Percentage					✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Field Goals	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Fouls	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Free Throw Attempts	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Free Throw Percentage											✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Free Throws	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Free Throw Rate					✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Games	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Games Started																					✓	✓
Minutes Played								✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Offensive Box Plus Minus														✓	✓	✓	✓	✓	✓	✓	✓	✓
Offensive Rebound Percentage															✓	✓	✓	✓	✓	✓	✓	✓
Offensive Rebounds														✓	✓	✓	✓	✓	✓	✓	✓	✓
Offensive Win Shares			✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Points	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Position	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Steal Percentage															✓	✓	✓	✓	✓	✓	✓	✓
Steals														✓	✓	✓	✓	✓	✓	✓	✓	✓
Team	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Total Rebounds Percentage													✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Total Rebounds							✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
True Shooting Percentage				✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Turnovers																✓	✓	✓	✓	✓	✓	✓
Turnover Percentage																		✓	✓	✓	✓	✓
Usage Percentage																	✓	✓	✓	✓	✓	✓
Value Over Replacement Player														✓	✓	✓	✓	✓	✓	✓	✓	✓
Win Shares			✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Win Shares 48									✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓

Each subset will be sent through a pipeline to generate classification models. The key components to this automation will be covered in more detail, but here is the overall process.

1. Create a response for each record.
   • 0: Player is not in the Hall of Fame
   • 1: Hall of Fame member
2. Split subset into balanced training and testing sets
3. Normalize the data
4. Perform a Principal Components Analysis (PCA) of the training set
5. Evaluate the PCA transformed data utilizing the following models:
   • Linear Discriminant Analysis
   • Logistic Regression
   • Naive Bayes
   • Quadratic Discriminant Analysis
6. Transform the test set using the classification model
7. Score the model

Create Response

This website was scraped to retrieve all the player Hall of Fame inductees through 2012. For the response, a value of one was assigned to the Hall of Famers, and a value of zero was given to all the other players.

• 1: Hall of Fame Player
• 0: Regular Player

Split Subset into Train Test Sets

The number of Hall of Fame records for each subset was grossly less than the regular player records, initially resulting in poor classification models. To remedy this issue, balanced training and test sets were generated using the following bootstrap technique.

1. For each feature, the data was standardized about the mean with a standard deviation equal to the variance.
2. Randomly segregate 20% of the found Hall of Fame records to be used as a Hall of Fame test set.
3. Randomly sample, with replacement, the remaining 80% of the Hall of Fame players until a training set with 500 records is generated. This means that multiple entries in this dataset will be identical.
4. Randomly sample the regular players until a Regular test set equal in size to the Hall of Fame test set from step 1 is generated.
5. Randomly sample, with replacement, 500 records from the regular players not included in the Regular test set. Here it is highly improbable that duplicate entries are included, but it still could happen.
6. Combine and shuffle the Hall of Fame test set with the Regular player test set.
7. Combine and shuffle the Hall of Fame training set with the Regular player training set.

Principal Components Analysis (PCA)

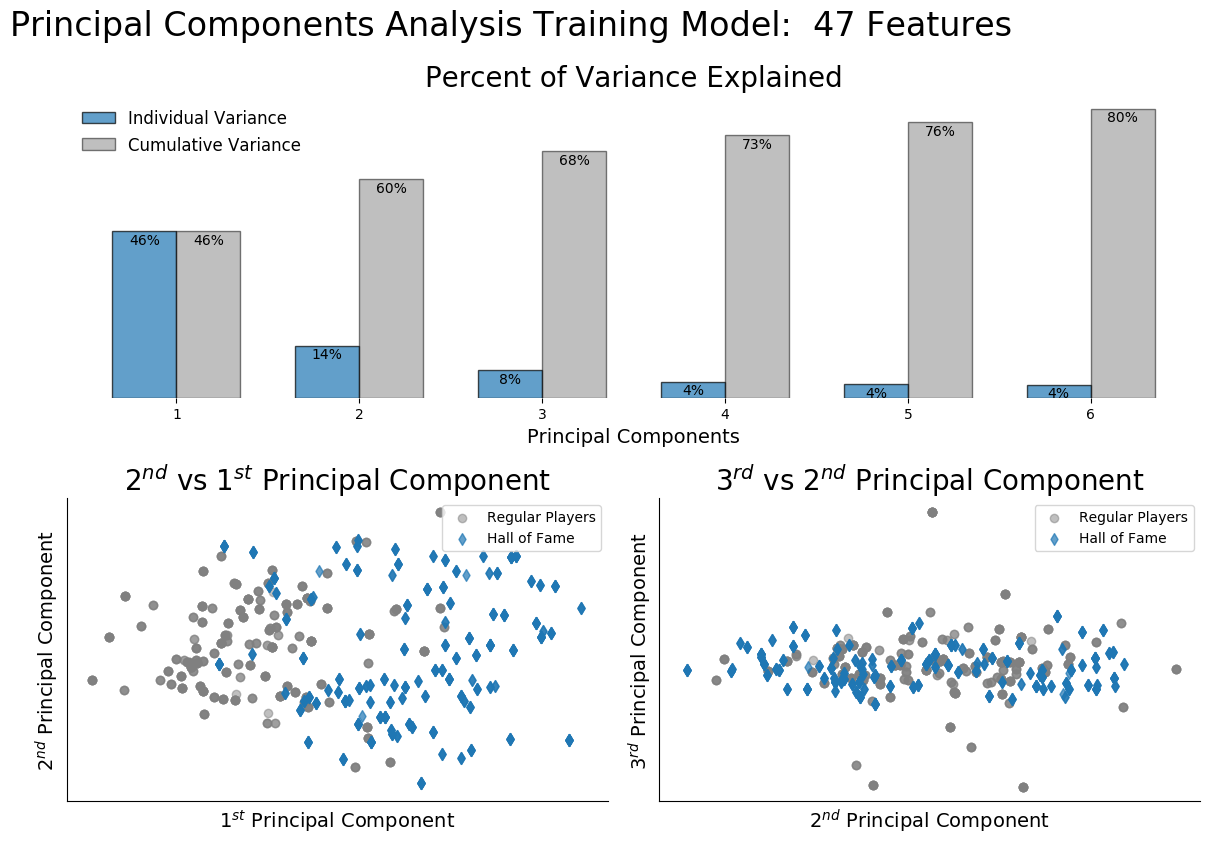
A Principal Components Analysis was performed on the test set for each subset to identify the components with maximum variance. This transformed space is normally used to reduce the number of features under consideration when generating a model, but due to the test set size of 1000 records, the computational time to keep all features was acceptable.

A summary plot for one of the subsets is shown below identifying the variance contribution of the most influential components and the first two hyperplanes of the PCA analysis. The influential components were chosen by including components where the first segment of the 2^nd derivative of the individual variance curve was positive.

Classification Models

With the subset transformed into the PCA space, it was now time to feed the data into the following classification algorithms.

• Linear Discriminant Analysis
• Logistic Regression
• Naive Bayes
• Quadratic Discriminant Analysis

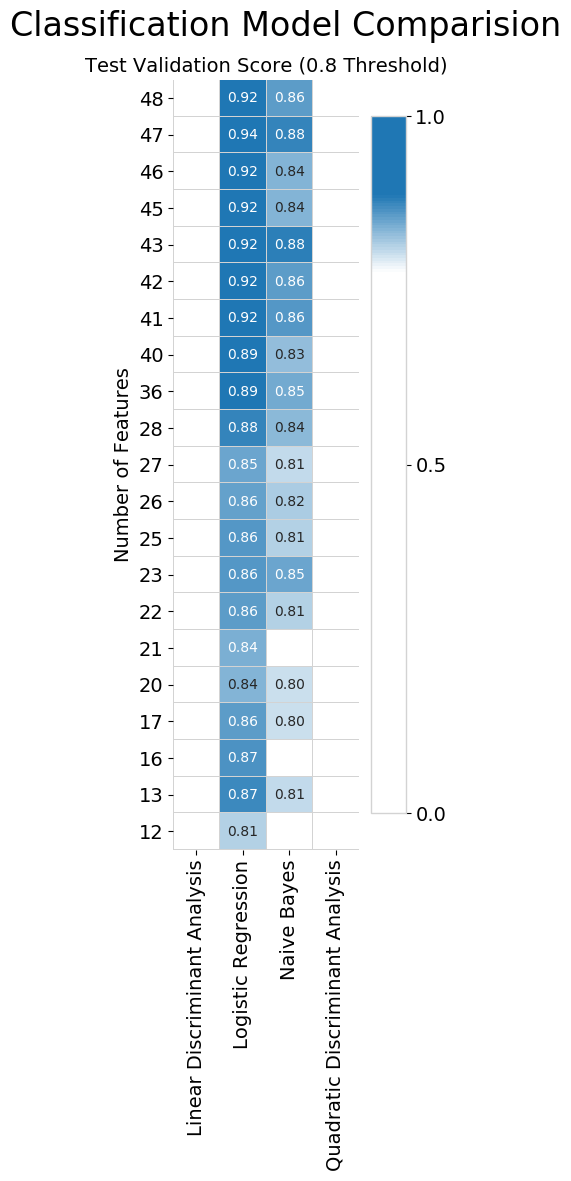
The next figure summarizes the predictive score for each model. If either the training or test score was below an accuracy of 80%, the subset was filtered out.

It's easily observed that the Logistic Regression model is the preferred choice for this dataset.

The subset utilizing 47 of the statistical features produced the highest predictive capability, but there is an element of stochastic variability involved in choosing the training and test sets. The machinery that analyzes this dataset has a default random seed value of zero chosen, which makes the results repeatable.

To verify the random seed value was not skewing the results, 100 instances of the Logistic Regression were run with the seed value allowed to be chosen at random. For each analysis, the subset with the highest accuracy was logged.

Here are the results of a particular batch.

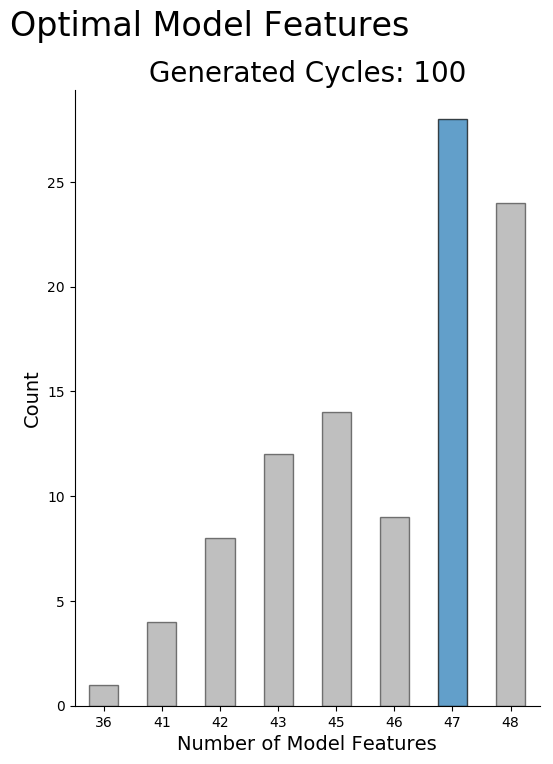
In some cases, the batch execution produced more high scores using the subset with 48 features than the subset of 47 features. The only difference between the two subsets was the feature 3-Point Field Goal Percentage. This information is captured in the combination of 3-Point Field Goals and 3-Point Field Goal Attempts, so I chose to use the subset of 47 features for future calculations.

The confusion Matrix generated from the test set using the preferred model of Logistic Regression and a subset of 47 features is below.

Now let's see what can be learned by applying our model to the entire subset of 47 features.

Application

Here is a list of the players classified as being Hall of Fame Worthy with the number predicted positive seasons in parentheses.

• Eddie Johnson (27)
• Mike Dunleavy (24)
• Chauncey Billups (22)
• Gerald Henderson (22)
• Vince Carter (22)
• Jason Kidd (22)
• Tim Hardaway (21)
• Andre Miller (21)
• Tim Thomas (21)
• Mark Jackson (20)
• Kobe Bryant (20)
• Sam Cassell (20)
• Dale Ellis (20)
• Ray Allen (20)
• Paul Pierce (19)
• Steve Blake (19)
• Joe Johnson (19)
• Allen Iverson (19)
• Beno Udrih (19)
• Peja Stojakovic (18)

Since our original Hall of Fame list only included inductees up to 2012, let's check if any of our predicted players actually made it in. Again, the number of predicted positive seasons will be in parentheses.

• Allen Iverson (19)
• Yao Ming (4)

From a total of 18 possible inductees, the model predicted only 2. This puts us 11% ahead of the default hypotheses that no one will be good enough to make the Hall of Fame.

To make an impact in the league, let's take a look at the players who have been pros for two years or less and have been identified as having Hall of Fame potential.

• A.J. Wynder
• Aaron Swinson
• Aleksandar Djordjevic
• Alex Abrines
• Allan Ray
• Alvin Heggs
• Alvin Sims
• Andre Emmett
• Andre Owens
• Andreas Glyniadakis
• Andy Rautins
• Anthony Grundy
• Arvydas Macijauskas
• Askia Jones
• Ben Hansbrough
• Bobby Cattage
• Bracey Wright
• Bryce Dejean-Jones
• Bryn Forbes
• Butch Graves
• Caris LeVert
• Carl Henry
• Carrick Felix
• Casper Ware
• Charles Thomas
• Chris Herren
• Chubby Cox
• Clint McDaniel
• Corey Crowder
• Craig Dykema
• D'Angelo Russell
• D.J. Kennedy
• D.J. Stephens
• Damir Markota
• Dane Suttle
• Dante Exum
• Darius Washington
• Darrun Hilliard
• Darryl Johnson
• Dave Johnson
• David Stockton
• Davis Bertans
• DeJuan Wheat
• Dedric Willoughby
• Demetrius Calip
• Demetrius Jackson
• Dennis Horner
• Dennis Nutt
• Denzel Valentine
• Derek Grimm
• Derrick Phelps
• Derrick Rowland
• Desmon Farmer
• Desmond Ferguson
• Devin Booker
• Dexter Boney
• Dijon Thompson
• Dionte Christmas
• Donald Whiteside
• Drew Gordon
• Dwight Anderson
• Ed Gray
• Evric Gray
• Fennis Dembo
• Forrest McKenzie
• Fred Vinson
• Gary Forbes
• Geno Carlisle
• Gerald Brown
• God Shammgod
• Guillermo Diaz
• Gundars Vetra
• Henry Ellenson
• Howard Carter
• Howard Nathan
• Ian Lockhart
• Igor Rakocevic
• Isaac Fontaine
• Ivan McFarlin
• Jabari Brown
• Jake Layman
• Jamal Murray
• James Collins
• James Cotton
• Jamie Waller
• Jarell Eddie
• Jay Edwards
• Jeffrey Sheppard
• Joe Crawford
• John Douglas
• John Greig
• John McCullough
• John Pinone
• Jonathan Gibson
• Josh Selby
• Juan Carlos
• Juan Hernangomez
• Karl-Anthony Towns
• Keith Appling
• Keith Smart
• Kelly Oubre
• Kim English
• Korleone Young
• Kyle Wiltjer
• Lamar Patterson
• Lance Allred
• Leonard Taylor
• Lionel Chalmers
• Logan Vander
• Lorenzo Charles
• Luis Montero
• Lynn Greer
• Malachi Richardson
• Malcolm Brogdon
• Malik Beasley
• Marcus Brown
• Marcus Georges-Hunt
• Marcus Vinicius
• Marcus Webb
• Marlon Garnett
• Matt Othick
• Matt Walsh
• Matt Wenstrom
• Melvin Sanders
• Mike Iuzzolino
• Mike Morrison
• Milt Wagner
• Mindaugas Kuzminskas
• Myron Jackson
• Nate Blackwell
• Nemanja Bjelica
• Nemanja Nedovic
• Nick Johnson
• Nicolas Laprovittola
• Nikita Wilson
• Nikola Jokic
• Norman Powell
• Oliver Robinson
• Orlando Graham
• Oscar Torres
• Pape Sy
• Pat Connaughton
• Patrick McCaw
• Pero Antic
• Peter John
• Peyton Siva
• Pierre Jackson
• Ratko Varda
• Raul Lopez
• Ray Blume
• Richard Petruska
• Richard Rellford
• Ricky Berry
• Ricky Grace
• Robert Hite
• Rock Lee
• Rodney McGruder
• Roger Powell
• Ryan Lorthridge
• Ryan Robertson
• Scott Machado
• Sergei Bazarevich
• Shane Heal
• Shea Seals
• Sheldon McClellan
• Sherell Ford
• Sherron Collins
• Skeeter Henry
• Steven Smith
• Stevin Smith
• Thomas Gardner
• Tim Quarterman
• Timothe Luwawu-Cabarrot
• Tom Sluby
• Treveon Graham
• Trevor Ruffin
• Troy Bell
• Uros Slokar
• Vander Blue
• Vassilis Spanoulis
• Vincenzo Esposito
• Wayne Turner
• Willie Warren
• Xavier Silas
• Yuta Tabuse

From a potential list of 1381 young players, the model has singled out 185 or 13% as potential greats. Identifying this subset would have a direct impact on the scouting and coaching staff with respect to piecing together a team designed for success.

Signing these players to medium term contracts would allow a team to be poised for multiple championship runs in the future.

Conclusion

This project looked at the NBA player statistics to generate a predictive model identifying potential Hall of Fame inductees. First, some characteristics of Hall of Fame players were presented. Then the details of creating a classification model were discussed. Finally, the derived model was employed to predict the next round of players to be inducted into the Hall of Fame in addition to singling out up and coming stars of the league.

Do you agree with the predictions? Who would you put in the basketball Hall of Fame? Leave a comment below and start the discussion!

Data Files

The following data files were used in the project.

Data File	Original Source
Naismith Memorial Basketball Hall of Fame List	NBA Website All Basketball Hall of Fame Inductees
Player Dataset	kaggle Website NBA Player Details
Season Statistics	kaggle Website NBA Player Metrics by Season

Source Code

Jupyter Notebook
Follow this link to view the project's notebook.

Python Modules
Follow this link to view the project's modules.

Note:
To create the geographic plots a Google API Key is required. The key is easy to obtain, but make sure to not share your key. For more details check out Google's site.

Versions

This study was completed using the Anaconda distribution of Python 3.6.2.